Оглавление:

• Основные теоретические сведения
  • Треугольник
  • Трапеция
  • Параллелограмм
  • Квадрат
  • Ромб и прямоугольник
  • Произвольные фигуры
  • Многоугольники
  • Окружность

 

Основные теоретические сведения

Треугольник

К оглавлению...

При решении задач по геометрии помимо всех геометрических формул и свойств, которые будут приведены ниже, нужно очень хорошо помнить основные формулы по тригонометрии. Укажем для начала несколько основных свойств различных типов углов:

• Смежные углы в сумме равны 180 градусов.
• Вертикальные углы равны между собой.

Теперь перейдем к свойствам треугольника. Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Запомните также, что сумма любых двух сторон треугольника всегда больше третьей стороны. Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы (медиана - линия проведенная через некоторую вершину и середину противоположной стороны в треугольнике):

Свойства медиан:

• Все три медианы пересекаются в одной точке.
• Медианы  делят  треугольник  на  шесть  треугольников  одинаковой  площади.
• В точке пересечения медианы делятся в отношении 2:1, считая от вершин.

Свойство биссектрисы (биссектриса - линия, которая делит некоторый угол на два равных угла, т.е. пополам):

Важно знать: Центр вписанной в треугольник окружности лежит на пересечении биссектрис (все три биссектрисы пересекаются в этой одной точке). Формулы биссектрисы:

Основное свойство высот треугольника (высота в треугольнике - линия проходящая через некоторую вершину треугольника перпендикулярно противоположной стороне):

Все три высоты в треугольнике пересекаются в одной точке. Положение точки пересечения определяется типом треугольника:

• Если треугольник остроугольный, то точка пересечения высот находится внутри треугольника.
• В прямоугольном треугольнике высоты пересекаются в вершине прямого угла.
• Если треугольник тупоугольный, то точка пересечения высот находится за пределами треугольника.

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Центр окружности описанной около треугольника лежит на пересечении посерединных перпендикуляров. Все три посерединных перпендикуляра пересекаются в одной этой точке. Посерединный перпендикуляр - линия проведенная через середину стороны треугольника перпендикулярно ей.

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c - гипотенуза, a и b - катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h - высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Подобные треугольники - треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т.п.) пропорциональны. Сходственные стороны подобных треугольников - стороны, лежащие напротив равных углов. Коэффициент подобия - число k, равное отношению сходственных сторон подобных треугольников. Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Признаки подобия треугольников:

• По двум углам. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
• По двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.
• По трём сторонам. Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

 

Трапеция

К оглавлению...

Трапеция - четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Длина средней линии трапеции:

Площадь трапеции:

Некоторые свойства трапеций:

• Средняя линия трапеции параллельна основаниям.
• Отрезок,  соединяющий  середины  диагоналей  трапеции,  равен  полуразности  оснований.
• В трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон находятся на одной прямой.
• Диагонали трапеции разбивают её на четыре треугольника. Треугольники, сторонами которых являются основания - подобны, а треугольники, сторонами которых являются боковые стороны - равновелики.
• Если сумма углов при любом основании трапеции равна 90 градусов, то отрезок соединяющий середины оснований равен полуразности оснований.
• У равнобедренной трапеции углы при любом основании равны.
• У равнобедренной трапеции диагонали равны.
• В равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой - полуразности оснований.

 

Параллелограмм

К оглавлению...

Параллелограмм - это четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Некоторые свойства параллелограмма:

• Противоположные стороны параллелограмма равны.
• Противоположные углы параллелограмма равны.
• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
• Сумма углов, прилежащих к одной стороне, равна 180 градусов.
• Сумма всех углов параллелограмма равна 360 градусов.
• Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.

 

Квадрат

К оглавлению...

Квадрат - четырёхугольник, у которого все стороны равны, а все углы равны по 90 градусов. Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Свойства квадрата – это все свойства параллелограмма, ромба и прямоугольника одновременно.

 

Ромб и прямоугольник

К оглавлению...

Ромб - это параллелограмм, у которого все стороны равны. Площадь ромба (первая формула - через две диагонали, вторая - через длину стороны и угол между сторонами):

Свойства ромба:

• Ромб является параллелограммом. Его противолежащие стороны попарно параллельны.
• Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
• Диагонали ромба являются биссектрисами его углов.

Прямоугольник - это параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника через две смежные стороны:

Свойства прямоугольника:

• Диагонали прямоугольника равны.
• Прямоугольник является параллелограммом - его противоположные стороны параллельны.
• Стороны прямоугольника являются одновременно его высотами.
• Квадрат диагонали прямоугольника равен сумме квадратов двух его не противоположных сторон (по теореме Пифагора).
• Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности.

 

Произвольные фигуры

К оглавлению...

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Обобщённая теорема Фалеса: Параллельные прямые отсекают на секущих пропорциональные отрезки.

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

 

Многоугольники

К оглавлению...

Выпуклым многоугольником называется многоугольник, обладающий тем свойством, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Сумма внутренних углов плоского выпуклого n-угольника равна:

Число диагоналей всякого многоугольника равно (где: n – число сторон):

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны. Внутренний угол правильного многоугольника равен:

Центральный угол правильного n-угольника равен:

Площадь правильного многоугольника с числом сторон n, длиной стороны a, радиусом описанной окружности R, полупериметром p и радиусом вписанной окружности r, может быть рассчитана по следующим формулам:

 

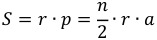
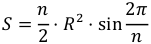
Окружность

К оглавлению...

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента: